All-pairs similarity via DIMSUM

We are often interested in finding users, hashtags and ads that are very similar to one another, so they may be recommended and shown to users and advertisers. To do this, we must consider many pairs of items, and evaluate how “similar” they are to one another.

We call this the “all-pairs similarity” problem, sometimes known as a “similarity join.” We have developed a new efficient algorithm to solve the similarity join called “Dimension Independent Matrix Square using MapReduce,” or DIMSUM for short, which made one of our most expensive computations 40% more efficient.

Introduction

To describe the problem we’re trying to solve more formally, when given a dataset of sparse vector data, the all-pairs similarity problem is to find all similar vector pairs according to a similarity function such as cosine similarity, and a given similarity score threshold.

Not all pairs of items are similar to one another, and yet a naive algorithm will spend computational effort to consider even those pairs of items that are not very similar. The brute force approach of considering all pairs of items quickly breaks, since its computational effort scales quadratically.

For example, for a million vectors, it is not feasible to check all roughly trillion pairs to see if they’re above the similarity threshold. Having said that, there exist clever sampling techniques to focus the computational effort on only those pairs that are above the similarity threshold, thereby making the problem feasible. We’ve developed the DIMSUM sampling scheme to focus the computational effort on only those pairs that are highly similar, thus making the problem feasible.

In November 2012, we reported the DISCO algorithm to solve the similarity join problem using MapReduce. More recently, we have started using a new version called DIMSUMv2, and the purpose of this blog post is to report experiments and contributions of the new algorithm to two open-source projects. We have contributed DIMSUMv2 to the Spark and Scalding open-source projects.

The algorithm

First, let’s lay down some notation: we’re looking for all pairs of similar columns in an m x n matrix whose entries are denoted a_ij, with the i’th row denoted r_i and the j’th column denoted c_j. There is an oversampling parameter labeled ɣ that should be set to 4 log(n)/s to get provably correct results (with high probability), where s is the similarity threshold.

The algorithm is stated with a Map and Reduce, with proofs of correctness and efficiency in published papers [1] [2]. The reducer is simply the summation reducer. The mapper is more interesting, and is also the heart of the scheme. As an exercise, you should try to see why in expectation, the map-reduce below outputs cosine similarities.

The mapper above is more computationally efficient than the mapper presented in [1], in that it tosses fewer coins than the one presented in [1]. Nonetheless, its proof of correctness is the same as Theorem 1 mentioned in [1]. It is also more general than the algorithm presented in [2] since it can handle real-valued vectors, as opposed to only {0,1}-valued vectors. Lastly, this version of DIMSUM is suited to handle rows that may be skewed and have many nonzeros.

Experiments

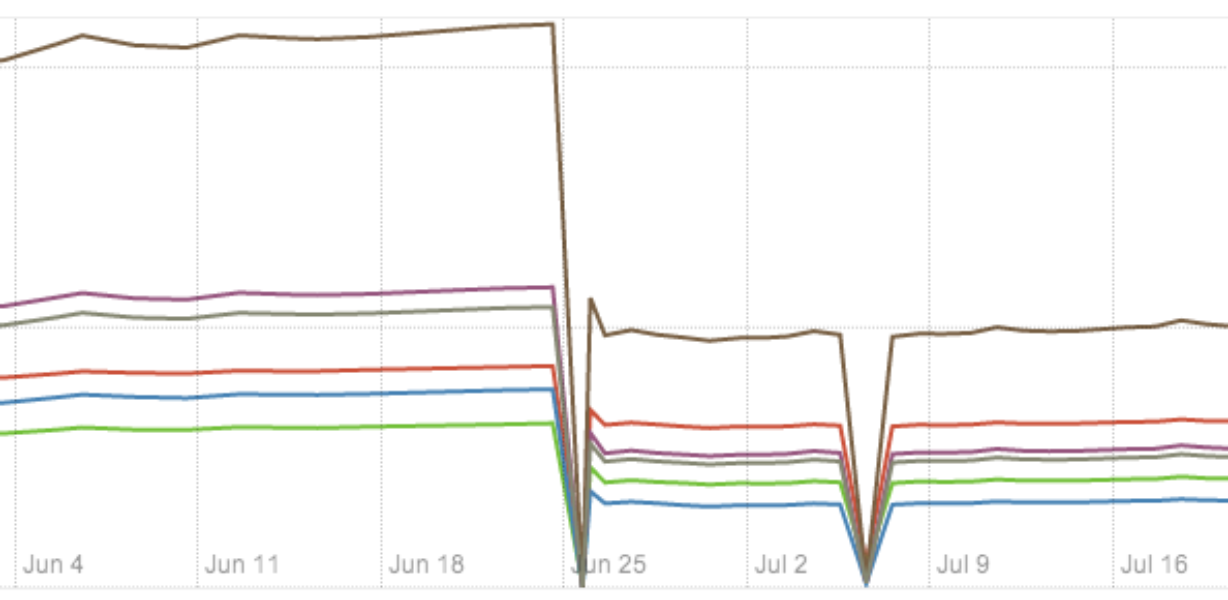
We run DIMSUM daily on a production-scale ads dataset. Upon replacing the traditional cosine similarity computation in late June, we observed 40% improvement in several performance measures, plotted below.

Open source code

We have contributed an implementation of DIMSUM to two open source projects: Scalding and Spark.

Scalding github pull-request: https://github.com/twitter/scalding/pull/833
Spark github pull-request: https://github.com/apache/spark/pull/336

Collaborators

Thanks to Kevin Lin, Oscar Boykin, Ashish Goel and Gunnar Carlsson.

References

[1] Bosagh-Zadeh, Reza and Carlsson, Gunnar (2013), Dimension Independent Matrix Square using MapReduce, arXiv:1304.1467

[2] Bosagh-Zadeh, Reza and Goel, Ashish (2012), Dimension Independent Similarity Computation, arXiv:1206.2082